 |
| 清智也准教授(撮影:近藤悦朗) |
科学技術の基幹となる普遍的な原理や方法論を探る数理情報学。なかでも、清智也准教授が専門に研究するのは、数理統計学と呼ばれる領域だ。自然現象や人間の活動など社会で起こる様々な問題を、統計学的なアプローチで読み解き、データに潜む情報を抽出し、モデル化し、その性質を調べることで、新たな視点を提案したり、未来を予測したりする。
研究を始めるきっかけは「なぜ」という疑問だ。ふだん当たり前と思ってきたことを、別の切り口で調べてみる。
清准教授が例にあげたのは、女子七種競技の得点法だ。100メートルハードル、走り高跳び、砲丸投げ、200メートル走、走り幅跳び、やり投げ、800メートル走の計7種目を2日間で競う陸上競技で、順位は、各種目の秒(時間)やメートル(距離)といった単位が異なる記録を、国際陸上競技連盟(IAAF)が定めるルールで数値化した得点を合算した総合点で決められる。
だが、その決め方は果たして、公平で、合理的なのか。統計的に、尤もらしいのか。 「簡単のため、100メートルハードル、200メートル走、やり投げの3種目について見てみましょう」
図1は、1991年~2013年の世界陸上の成績から抜粋した5人の選手の記録(左)で、それらをIAAFのルールで数値化したのが右側の得点だ。
| ※ページ内の画面をクリックして拡大画像をご覧下さい |
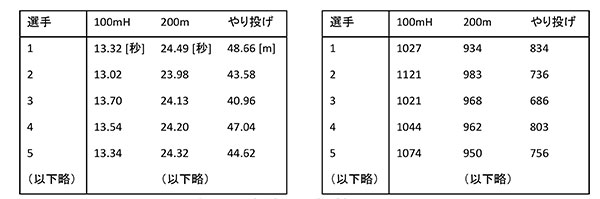 |
図1 女子七種競技のうち、100メートルハードル(100mH)、200メートル走(200m)、やり投げのデータ。1991年~2013年の世界陸上の成績から抜粋した5人の選手の記録(左)と、IAAFのルールで数値化したもの(右)
統計学の基本的な考え方として「標準得点」がある。これは学力を測るときに使われる「偏差値」と同じものだ。そこで、IAAFのルールの代わりに、標準得点の合計を総合点と考えたらどうか? 実は、この方法は必ずしも妥当とは言えない。3種目の得点間の相関係数をとると[図2]、100メートルハードルと200メートル走の相関は大きいが、これら二つとやり投げは相関がほとんどないことがわかる。つまり、100メートルハードルが得意な選手は200メートル走も得意で、標準得点の合計は短距離が得意な選手に有利になってしまうと考えられるのだ。その結果は我々の直感とも一致する。
| ※ページ内の画面をクリックして拡大画像をご覧下さい |
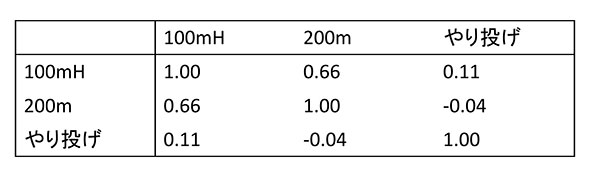 |
図2 3種目の得点の相関係数行列。100メートルハードルと200メートル走の相関は大きいが、やり投げは相関がほとんどない。
それを視覚化したのが、「やじろべえ」のような図だ[図3]。3本の腕が各種目に相当し、腕同士のなす角度(の余弦)が相関係数に対応する。三つのおもりの重さは同じ。標準得点の場合、やり投げを表すおもり(青)の位置が他の2種目に比べて高い(左)。逆に、IAAFのルールではやり投げの位置が少し低くなる(中)。公平にするには、三つのおもりの位置を調節して、できるだけ水平になるようにすればよい(右)。
| ※ページ内の画面をクリックして拡大画像をご覧下さい |
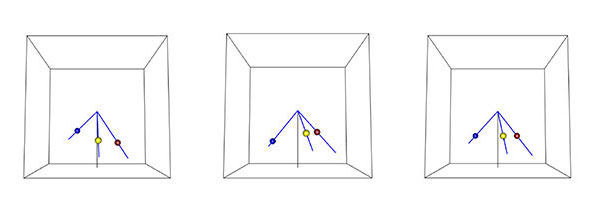 |
図3 3種目の得点の相関係数を、「やじろべえ」で表した図。3本の腕はそれぞれの種目に相当し、腕同士のなす角度(の余弦)が相関係数に対応する。おもりの色は茶色が100メートルハードル、黄色が200メートル走、青がやり投げを表す。左と中央の図は不公平のイメージ。公平にするためには、右の図のように、三つのおもりができるだけ水平になるよう、調整すればよい。
公平にするために導入したのは、相関係数行列と重みベクトル、その対角行列を用いる考え方だ。重みベクトルをいろいろ変えると、一つの解が見つかる。清准教授は、それを「客観的総合指数(OGI= Objective General Index)」と名付けた[図4]。
| DSDe=e |
図4 客観的総合指数(OGI)の方程式。Dは重みを表す未知の対角行列、Sは相関係数行列、eはすべての成分が1の列ベクトル。この解が一意に決まることは、50年ほど前の研究で明らかにされていた
この考え方で7種目について計算した結果が図5だ。左の図はIAAFルールに従って総合得点を算出するときの「やじろべえ」、右の図はOGIに基づいておもりの位置を変えた場合の「やじろべえ」を表す。OGIを使うとおもりの位置が水平になるのに対し、IAAFのルールでは走り幅跳び(緑)がやや有利で800メートル走(紫)がやや不利、という結論となった。
| ※ページ内の画面をクリックして拡大画像をご覧下さい |
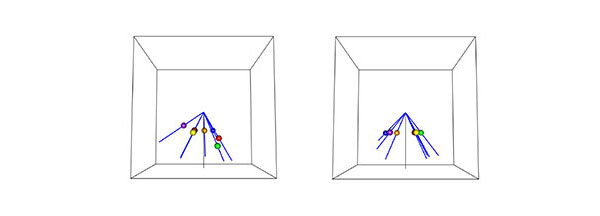 |
図5 実際に7種目で計算した図。IAAFルールに従った場合(左)とOGIに基づく場合(右)。OGIを使うとおもりの位置が水平になるのに対し、IAAFのルールでは走り幅跳び(緑)がやや有利で800メートル走(紫)がやや不利、という結論となる。
方程式自体は、すでに50年ほど前に調べられ、数学的に解が一意に存在することも示されていたが、いま、清准教授は、OGIをいろいろな分野に応用できないだろうかと考えている。株価の指標などの金融、成績や入試の配点、大学のランキングなどの教育、医療統計やエネルギー需要の予測など……。「従来とは違う、新たな視点のヒントを提供できるかもしれません」
数理統計学を志すようになったのは、工学部計数工学科の3年生の頃。脳神経科学者で、現在は独立行政法人理化学研究所脳科学総合研究センター特別顧問の甘利俊一さんが提唱した「情報幾何」を知った。
 |
| 「情報幾何」について語る清准教授 (撮影:近藤悦朗) |
確率分布を一つの情報要素として、その集まりが作る空間の持つ幾何学構造を調べることで、仕組みを理解しようという考え方。一見、関係性がないように見える情報も、幾何の世界に投影すると、イメージが明確になり、見通しがよくなる。
「たとえば、平均値は同じでも、狭く中心に集まった分布もあれば、だらりと広がった分布もある。距離という幾何の概念を持ち込むと、ぼうっとしていたものがはっきりと見えてくるのです」
もともと数学は好きで、統計学への興味もあった。情報と幾何をつなぐ新しい方法論に魅力を感じた。
以来、統計モデルの研究に取り組んできた。博士課程修了後、情報理工学系研究科の助手をへて、2011年から4年間慶應義塾大学理工学部で教鞭をとり、2015年春、母校に戻ってきた。現在は、「ホロノミック勾配法」や「最適輸送」「変数変換」「不均衡データ」などのテーマに関心を持って研究を進めている。
キーワードは「少しだけ見方を変えてみる」こと。複雑な現象を目の前にして、一筋縄ではいかない統計モデルを相手にしたとき、一般のユークリッド空間ではない空間に置き換えたり、性質がよくわかっている関数や多項式に当てはめたり、変数変換をしたり……。その結果、高次元の積分を避けられるなど、比較的計算しやすいモデルが得られて、糸口が見つかる場合がある。
心にとめているのは、2016年春に東大を退職した統計学の竹村彰通教授の言葉。「いきなり一般的に解こうとせず、まず小さい問題を考えなさい」というものだ。
一般化したいならば、具体的なところから始めてみる。いきなり大きな難題に取り組んでも、すぐにスマートな答が見つかるはずはない。まず解けそうな問題からやってみる。簡単なモデルに当てはめてみると、ヒントが見つかるかもしれない。うまく行けば、より大きな問題に広げてみる。だめなときはモデルが悪いのだから、もう一度最初からやり直す。
実際の研究は、そうした試行錯誤の繰り返しだ。
「それだけに、美しい答、美しいモデルを見つけたときは感激します」
自身が指導する立場になって、学生たちには、「言われたことをやるだけでなく、自分で調べること。わかったつもりにならず、自分で考えること。これまでにだれかがやったのとは違う視点、違う方法を試みること」と話す。
演習や輪講は、学生たちと自由な発想でアイデアを出し合い、議論をする場だ。OGIを思いついたのも、院生と相関係数行列について議論をしたのがきっかけだった。経済学など異分野の研究者と話すことも、大きな刺激となる。
情報理工学という「実学」として、扱うのは、基礎から応用まで、地球規模の問題から身近な問題まで、あまねく現実世界の現象のデータだ。
学生を指導した修士論文や卒業研究のタイトルにも、「空間点過程データの残差解析」や「ベイズ推測のためのマルコフ連鎖モンテカルロ法」といった統計学手法の基礎となるものもあれば、「多変量自己回帰モデルを用いた電力需要予測」や「疾病地図の作成と空間集積性の検定」などのエネルギーや医療分野への応用、さらには「習字データの解析――見本との類似性の定量化」「野球選手の攻撃的能力の分散分解」など、ユニークなものも並ぶ。
これらはバラバラなようで、一つ一つすべてが数理統計学という木の枝を形作っている。
「しっかりと地に根差し、幹を太く、枝葉を豊かに茂らせたい」
(2016年3月/取材・構成:五十嵐道子)
![]() 清智也准教授のホームページ
清智也准教授のホームページ
http://www.stat.t.u-tokyo.ac.jp/~sei/

Copyright © 2019 Graduate School of Information Science and Technology, The University of Tokyo